La régression vers la moyenne : 2 astuces pour en tirer profit en investissement
La "régression vers la moyenne" est un concept méconnu et pourtant très important en investissement. Voici comment en tirer profit dans le domaine de la bourse.
Qu'est-ce que la "régression vers la moyenne", ou "mean reversion" en anglais? Il s'agit en fait d'un concept assez méconnu et pourtant très important en investissement. Voyons comment nous pouvons l'utiliser pour en tirer profit dans le domaine de la bourse.
En tant que Partenaire d'Amazon, je suis rémunéré(e) pour les achats éligibles. Cela ne change rien pour vous mais permet de soutenir la gratuité de ce blog.
Pour commencer, voici une définition de la régression vers la moyenne par Wikipédia :
En statistique, la régression vers la moyenne décrit le phénomène suivant : si une variable est extrême à sa première mesure, elle va généralement se rapprocher de la moyenne à sa seconde mesure.
Si elle est extrême à sa seconde mesure elle va tendre à être proche de la moyenne à sa première mesure.
Afin d'éviter des inférences erronées, la régression vers la moyenne doit être considérée à la base de la conception des expériences scientifiques et prise en compte lors de l'interprétation des données.
Que signifie la régression vers la moyenne?
Francis Galton fût le premier à théoriser la régression vers la moyenne avec son article paru en 1886 et qui s'intitule Régression vers la médiocrité dans la stature héréditaire.
À noter que Galton est également le père du concept de sagesse des foules.
Selon lui, la taille d’un enfant est due en partie à la taille de ses parents, et en partie au hasard.
Cependant, Galton remarqua lors d’une observation que les enfants de parents dits « grands » avaient une taille qui restait malgré tout plus proche de la moyenne. Ils étaient donc plus petits que leurs parents.
En outre, les enfants de parents dits « petits » avaient aussi une taille proche de cette fameuse moyenne et étaient donc plus grands vis-à-vis de leurs propres géniteurs.
En d’autres termes, pour imager la chose :
Si les parents faisaient en moyenne 190 cm, l’enfant faisait plutôt 170 cm et si les parents faisaient en moyenne 150 cm, l’enfant était malgré tout assez proche des 170 cm.
Notez que même si ceci fonctionne sur une échelle globale, il y a bien entendu quelques exceptions. Exemple : des parents qui feraient en moyenne 190 cm et dont l’enfant mesurerait 210 cm.
Cette observation constitue donc la régression vers la moyenne.
La régression vers la moyenne peut se transposer à deux reprises dans le milieu de l’investissement et de la bourse :
La régression vers la moyenne dans la croissance et les retours sur capitaux
Imaginez que vous trouvez une superbe entreprise. Elle possède une belle croissance, ainsi qu’un retour sur capitaux attrayant. Vous remarquez même qu'elle se démarque de la concurrence grâce au niveau attrayant de ces deux caractéristiques.
La régression vers la moyenne est évidemment présente dans ces deux caractéristiques tellement attirantes qu'elles ne sont pas « habituelles » ou du moins semblables à la moyenne des taux de croissance et des retours sur capitaux des autres sociétés.
Tôt ou tard, votre entreprise rejoindra malheureusement la moyenne des entreprises de son secteur, pays, etc... Mais à quelle vitesse ?
Voici le return on invested capital (ROIC) des entreprises non-financières après 15 années. On voit bien ici que les courbes ont tendances à se resserrer vers la moyenne.
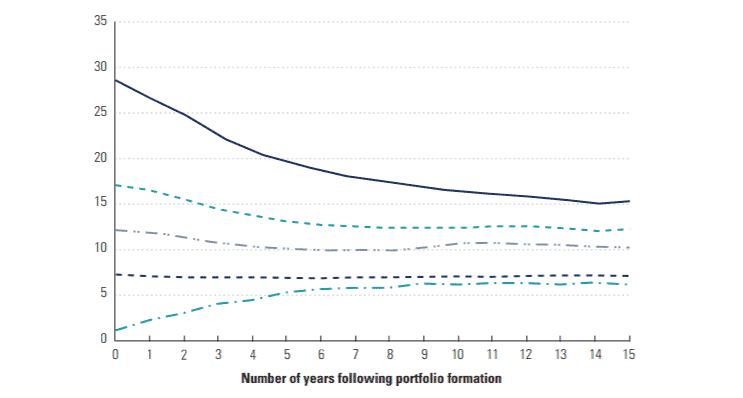
Voici le même phénomène, mais uniquement sur les entreprises actives dans les biens de consommations non-cycliques (produits d’hygiène, alcool, boissons, etc).
Nous pouvons donc voir qu’une fameuse régression vers la moyenne se forme. Les entreprises ayant au départ un très grand ROIC tendent avec le temps à se rapprocher d’une moyenne plus proche des autres entreprises et vise-versa pour les entreprises ayant au départ un ROIC très faible.
Cependant, il faut constater que cette régression vers la moyenne se fait de manière lente. Et en général, une entreprise affichant un ROIC élevé, tend à conserver un ROIC plus grand que les autres entreprises de son secteur.
Passons maintenant à la régression vers la moyenne concernant la croissance :
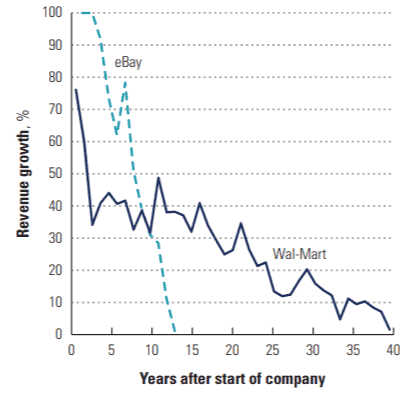
Voici l’historique de croissance pour l’entièreté des secteurs :
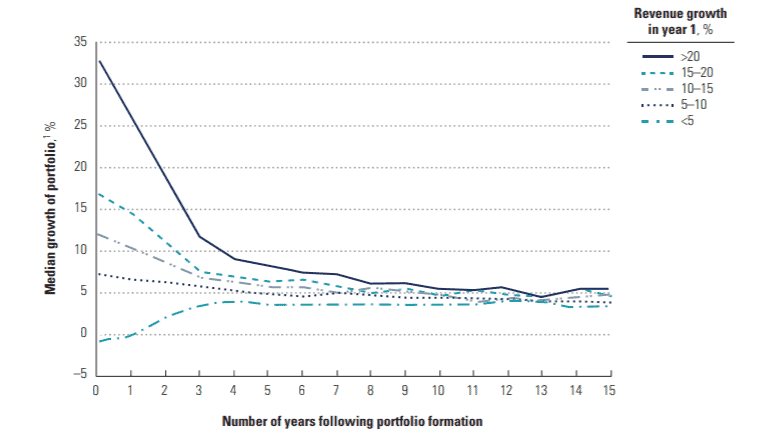
La régression vers la moyenne se fait ici de manière beaucoup plus brutale et est très rapide.
Les auteurs du graphique ajoutent d'ailleurs :
Only 26 percent of high-growth companies maintained better than 15 percent real growth 10 years later. High growth is very difficult to sustain—much more difficult than high ROIC.
N’oubliez pas que la régression vers la moyenne est un concept global, ce qui implique que plusieurs entreprises arriveront à remettre en question cette régression.
En effet, comme l’expliquent les auteurs du livre Valuation, 26% des entreprises de grande croissance parviennent à maintenir une croissance d’au moins 15%. Dans ces 26% on pourrait donc citer Google, Facebook, etc. Cependant 74% n’arriveront pas à tenir cette croissance.
Nous pouvons donc en conclure : Est-ce vraiment intéressant d’acheter une entreprise qui possède une croissance démesurée uniquement sur base de cette donnée ? Je vous laisse vous faire votre propre opinion.
Fait positif, le ROIC, qui est un des fondements de la stratégie appliquée par Buffett (notamment), est également sujet à la régression vers la moyenne.
Acheter une entreprise pour un ROIC deux fois supérieur à ses concurrents m'apparaît de toutes manières déjà beaucoup plus pragmatique.
La régression vers la moyenne comportementale
Dans cette dernière partie, nous allons voir que la régression vers la moyenne est également présente dans notre psychologie comportementale et va donc venir influencer le cours des actions.
Richard Thaler et Werner Debondt se sont posés une question :
- Est-ce que les investisseurs ont tendance à sur-réagir à l’information ?
Ils se sont donc amusés à créer une multitude de portefeuilles. Cependant deux classes seraient bien distinctes :
- La première classe serait constituée de portefeuilles d’actions contenant des entreprises qui ont sous-performé le marché durant les derniers mois/années.
- La seconde classe serait constituée de portefeuilles d’actions contenant des entreprises qui ont surperformé le marché.
A noter que pour Thaler et Debondt, un gagnant est une entreprise ayant eu une performance plus élevée que le marché ainsi qu’un PER plus haut que le marché.
Voici le test entre 1933 et 1980, soit sur 47 ans, séparés en blocs de 3 années. La durée moyenne de détention est de 3 ans :
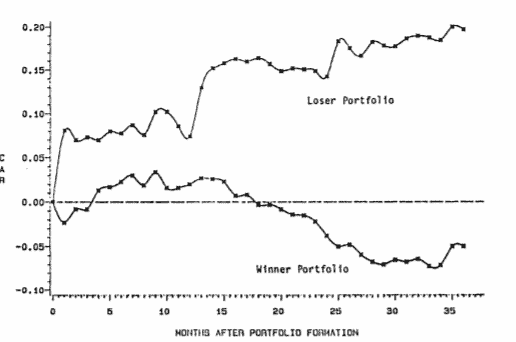
Nous pouvons voir que les portefeuilles n’ayant que des perdants historiques ont surperformé les portefeuilles ne détenant que des « gagnants ».
Voici le résultat lors d’une détention égale à 5 années :
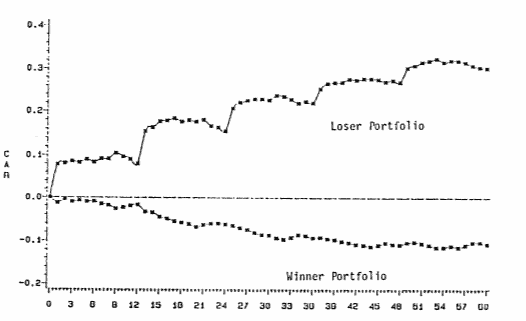
Ce que Richard Thaler et Werner Debondt ont voulu démontrer avec leur étude est littéralement la chose suivante :
Les acteurs du marché ont-ils tendance à sur-réagir lors de bonnes et mauvaises nouvelles ? La réponse est oui.
Ils expliquent que ce phénomène est en outre lié principalement à la régression vers la moyenne.
Pour conclure, voici quelques exemples (non-exhaustifs) de régression vers la moyenne tirée du livre Système 1, système 2.
Du moment que la chance joue un grand rôle, le succès d'une entreprise ne permet pas de conclure à la qualité de sa direction et des pratiques de management.
Et même si vous saviez parfaitement à l'avance d'un PDG a des idées géniales et des compétences hors du commun, vous n'en seriez pas moins incapable de prédire comment sa société va se comporter, la précision de vos prévisions revenant en gros à jouer à pile ou face.
En moyenne, la différence, en termes de profitabilité et de rendement boursier, entre les deux groupes de sociétés (celles à succès et les autres) passées en revue par Built to Last s'est presque annulée dans la période qui a suivi la publication de l'étude.
La profitabilité moyenne des sociétés identifiées dans le célèbre In Search of Excellence (En Quête de l'Excellence) de Thomas Peters et Robert Waterman a elle aussi chuté nettement peu de temps plus tard.
Une étude des "Sociétés les plus admirées" réalisée par le magazine Fortune montre que sur une période de vingt ans, les sociétés les plus mal classées ont ensuite atteint des rendements boursiers supérieurs à ceux des sociétés les plus admirées.
Peut-être avez-vous tenté de trouver des explications causales à ces observations : peut-être les entreprises à succès ont-elles fait preuve de complaisance, peut-être celles qui marchaient moins bien ont-elles redoublé d'efforts.
Mais ce n'est pas sous cet angle qu'il faut aborder ce qui s'est passé. La différence moyenne ne peut que se réduire, parce que la différence de départ était due en grande partie à la chance, qui a contribué tant au succès des unes qu'aux mauvaises performances des autres. Nous avons déjà rencontré cette réalité statistique : la régression vers la moyenne.
Si les récits sur l'ascension et la chute des entreprises trouvent un tel écho auprès des lecteurs, c'est qu'ils leur offrent ce dont a besoin l'esprit humain : un message simple, mettant en scène le triomphe et l'échec, identifiant des causes claires et taisant le pouvoir déterminant de la chance et l'inévitabilité de la régression.
Ces histoires suscitent et entretiennent une illusion de compréhension, et administrent des leçons qui n'ont à terme que peu de valeur à des lecteurs qui ne demandent qu'à les croire.
Vous êtes le prévisionniste des ventes d'une chaîne de supermarchés. Toutes les boutiques sont de même taille et proposent les mêmes articles, mais leurs ventes diffèrent pour des questions d'emplacement, de concurrence et de facteurs aléatoires.
On vous transmet les résultats pour 2011 et on vous demande de prédire les ventes pour 2012. On vous a recommandé d'accepter la prédiction d'ensemble des économistes, qui assurent que les ventes vont globalement augmenter de 10%.
Comment compléteriez-vous ce tableau?
| Magasin | 2011 | 2012 |
| 1 | 11.000.000 $ | - |
| 2 | 23.000.000 $ | - |
| 3 | 18.000.000 $ | - |
| 4 | 29.000.000 $ | - |
| Total | 81.000.000 $ | 89.100.000 $ |
Après avoir lu ce chapitre, vous savez que la solution évidente, qui consiste à ajouter 10% aux ventes de chaque magasin, est erronée.
Il faut que vos prévisions soient régressives, ce qui signifie ajouter plus de 10% aux succursales dont les performances sont plus faibles, et moins (voire retrancher un certain montant) aux autres.
Mais si vous posez la question à d'autres personnes, vous allez sans doute vous heurter à leur perplexité : pourquoi venir les ennuyer avec une question évidente?
Comme Galton l'avait découvert à ses dépens, le concept de la régression est loin d'être évident.
Les sources d'inspiration pour l'article
Le livre Valuation : Measuring and Managing the Value of Companies 6 ème édition de Tim Koller, Marc Goedhart et David Wessels.
Le livre Système 1, système 2 de Daniel Kahneman.
Les études de Richard H. Taler et Werner F. M. De Bondt :
- A mean-reverting walk down the Street
- Does the stock market overreact ?
Le papier Francis Galton and regression to the mean.
Avertissement : Cette analyse sur les biotechs américaines est une indication, et aucunement un conseil d'achat. Par conséquent, l’auteur ne pourra être tenu responsable en cas de pertes sur le(s) produit(s) concerné(s). Tout investissement comporte des risques de pertes. Pour plus d’infos, voyez nos mentions légales.
Si vous ne voulez rater aucun nouvel article, abonnez-vous à ma newsletter ci-dessous, likez ma page Facebook et suivez-moi sur Threads.